Implementation and Convergence Analysis of First-Order Optimization Methods for a CNN

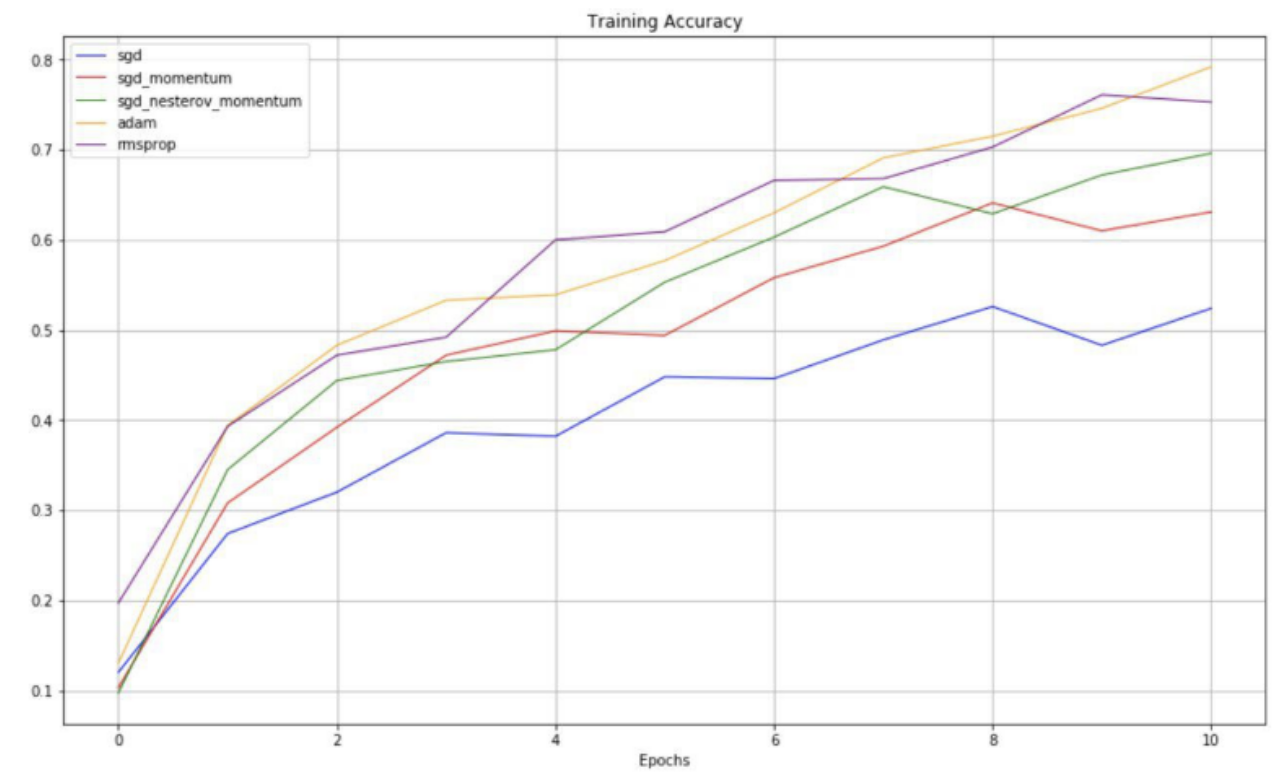
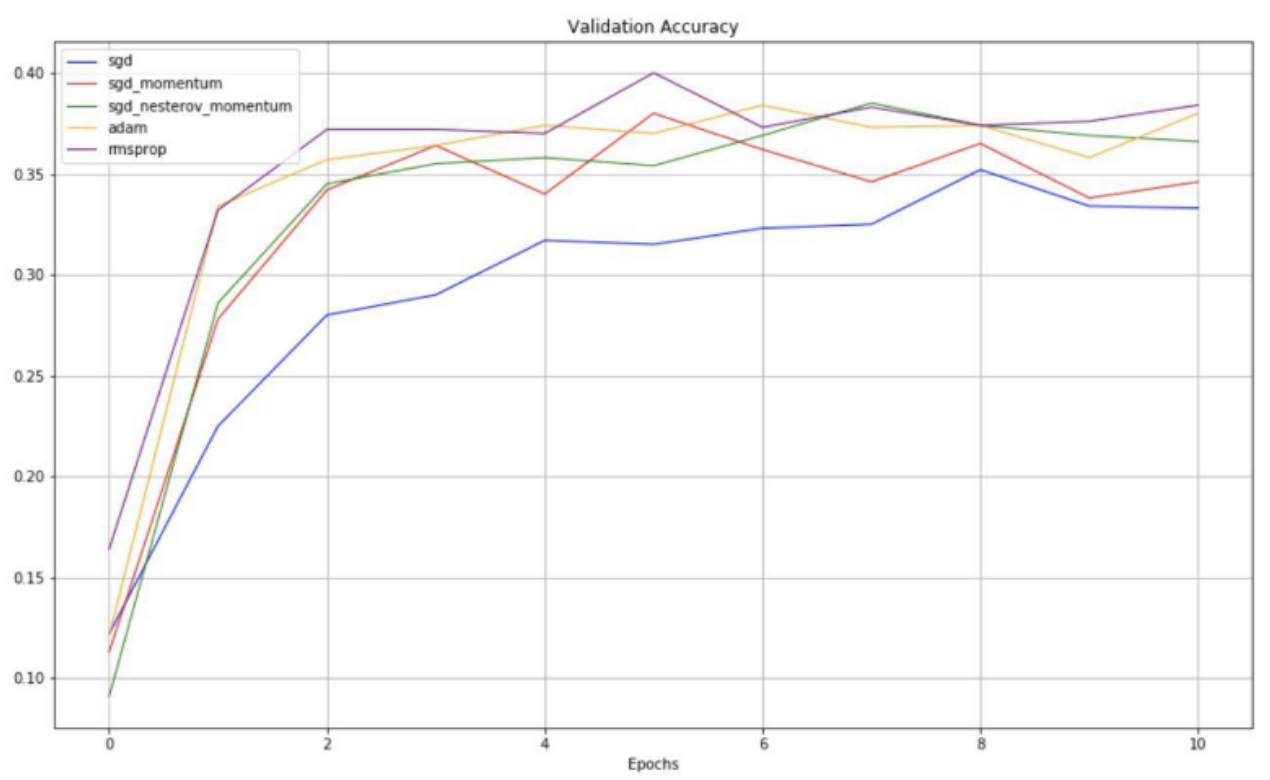
The Full Paper has a Python implementation of 5 first-order optimization methods: stochastic gradient descent (SGD), stochastic gradient descent with momentum (SGD-M), stochastic gradient descent with Nesterov momentum (SGD-NM), root mean square prop (RMSprop), and Adam. I perform a convergence analysis and discuss why the results confirm the distinguishing characteristics of the first-order methods discussed in the Methods section. Adam and RMSprop exhibit the best convergence and prove to be the best first-order optimization methods for a fully-connected neural network applied to a CIFAR-10 classification task.

To reduce noise in the convergence graphs, a subsample of 4,000 images was used from the CIFAR-10 dataset. Hence an epoch in these plots represents one run through this subsampled dataset. As we run 10 epochs of training with batch sizes of 100 samples, the plots below of the training loss are accordingly over 400 iterations of training, i.e. 400 parameter updates for each of the first-order methods.

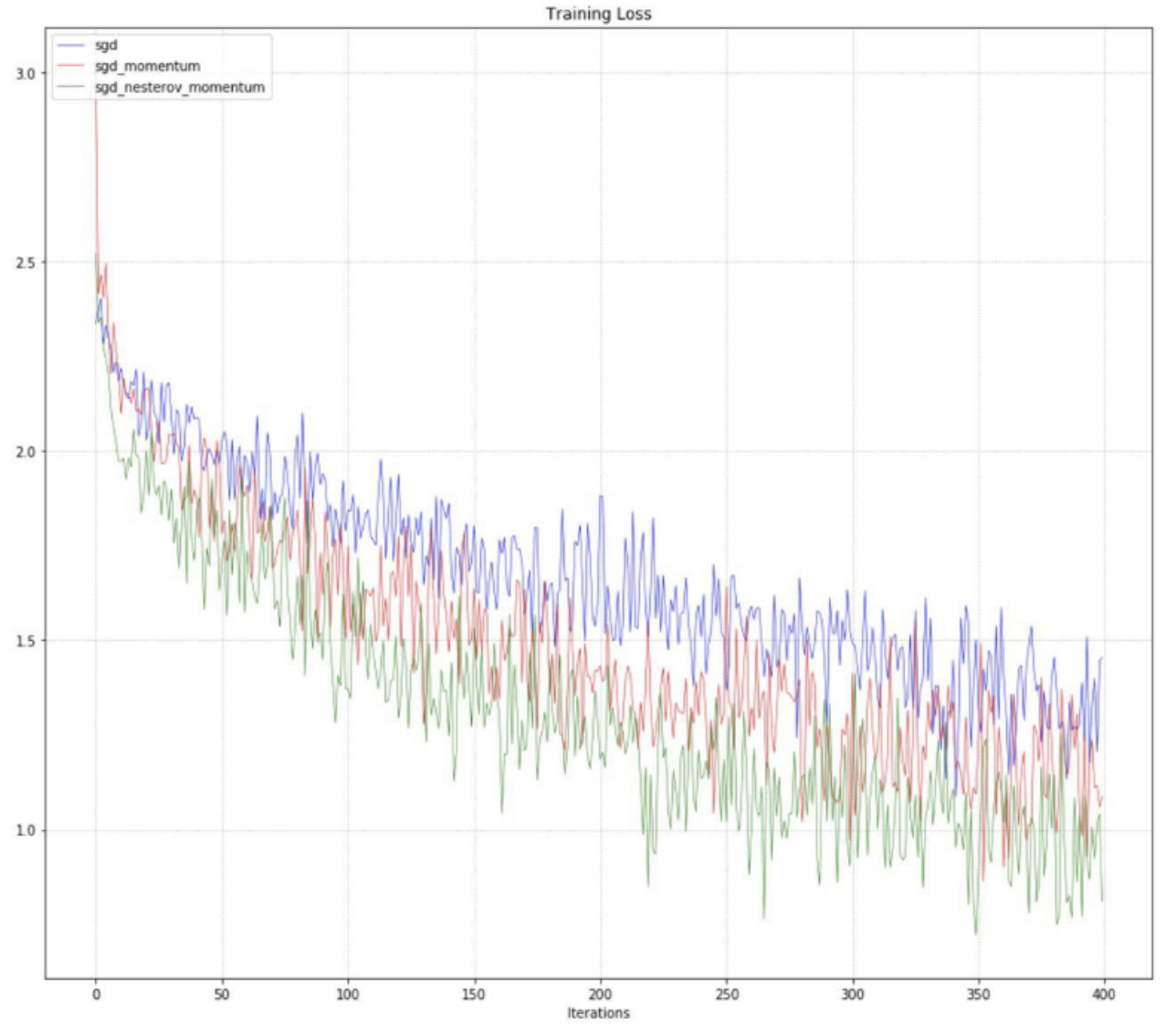
First we can observe the training loss for SGD, SGD-M, and SGD-NM over iterations of gradient descent.

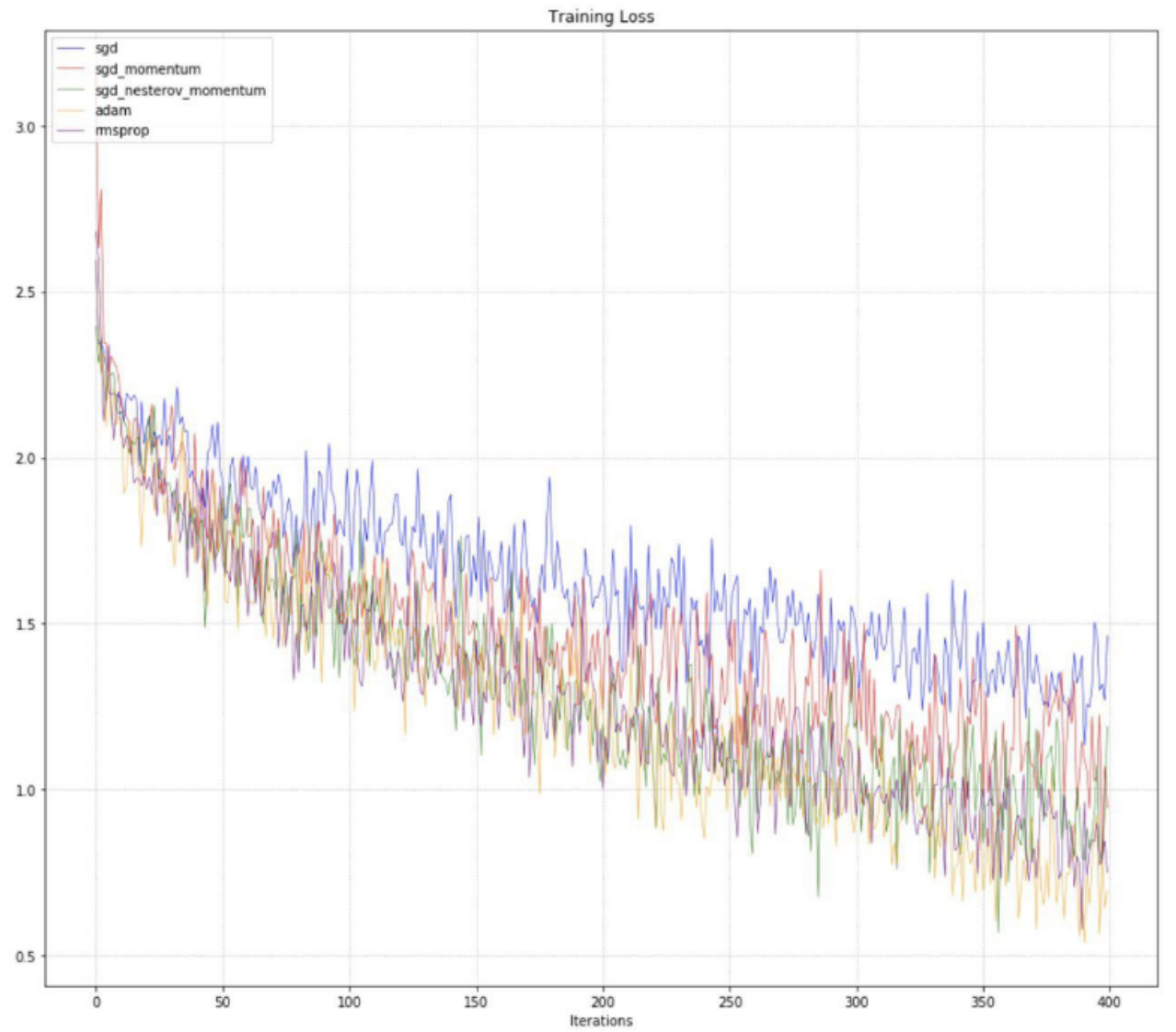
Next we can see the training loss for SGD, SGD-M, SGD-NM, RMSprop, and Adam over iterations of gradient descent.

And these are the training and validation accuracies for SGD, SGD-M, and SGD-NM over epochs.

As expected between SGD, SGD-M, and SGD-NM, SGD makes the slowest progress in minimizing the objective function value, or the training loss, over iterations. And SGD-NM exhibits improved convergence over SGD-M, as it only improves SGD-M with the key notion that the gradient dw is computed at the “lookahead” position of the parameters w, where the momentum step will soon take us.

We can also observe that RMSprop and Adam tend to perform slightly better than SGD-NM on this specific neural network problem, with Adam (orange) exhibiting the best convergence, i.e. the lowest training loss, after 400 iterations. We can see the training loss of the orange line falling steadily below RMSprop (purple) and SGD-NM (green), especially toward the later stages of training.